13. Roman to Integer

題目描述：
羅馬數字包含以下七種字符：I、V、X、L、C、D 和 M。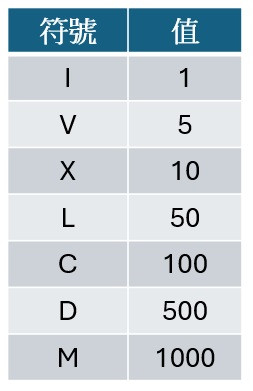

例如，羅馬數字 2 寫作 II，即為兩個並列的 1。12 寫作 XII，即為 X + II。27 寫作 XXVII，即為 XX + V + II。

通常情況下，羅馬數字中較小的數字在較大的數字右邊。但也存在特例，例如 4 不寫作 IIII，而是 IV。數字 1 在數字 5 的左邊，表示 4。同樣地，數字 9 表示為 IX。這種特殊規則只適用於以下六種情況：

I 可以放在 V（5）和 X（10）的左邊，來表示 4 和 9。
X 可以放在 L（50）和 C（100）的左邊，來表示 40 和 90。
C 可以放在 D（500）和 M（1000）的左邊，來表示 400 和 900。
給定一個羅馬數字，將其轉換為整數。
解題思路：
絕大多數人對羅馬數字並不陌生，但可能僅限於理解 1 到 10 之間的範圍。通過這道題目，我們可以仔細觀察羅馬數字的邏輯，並進一步瞭解其背後的原理，這樣才能將其轉換為對應的整數。

首先，我們注意到羅馬數字中的特殊組合，例如 IV 和 VI，這兩者都是由 I 和 V 組成，但由於 I 的位置不同，代表的數值也不同。如果 I 放在 V 的左邊（即 IV），那麼 I 表示的是減法，結果是 5 - 1 = 4。相反，如果 I 放在 V 的右邊（即 VI），那麼 I 表示的是加法，結果是 5 + 1 = 6。

換言之，在轉換羅馬數字為整數的過程中，我們需要檢查每個符號與其相鄰符號之間的關係。如果當前符號代表的數值比其後一個符號的小，那麼我們應該執行減法；否則，我們應該執行加法。如果是超過三個以上的羅馬數字，無論我們從左往右計算或是從右往左計算，其結果都是一樣的。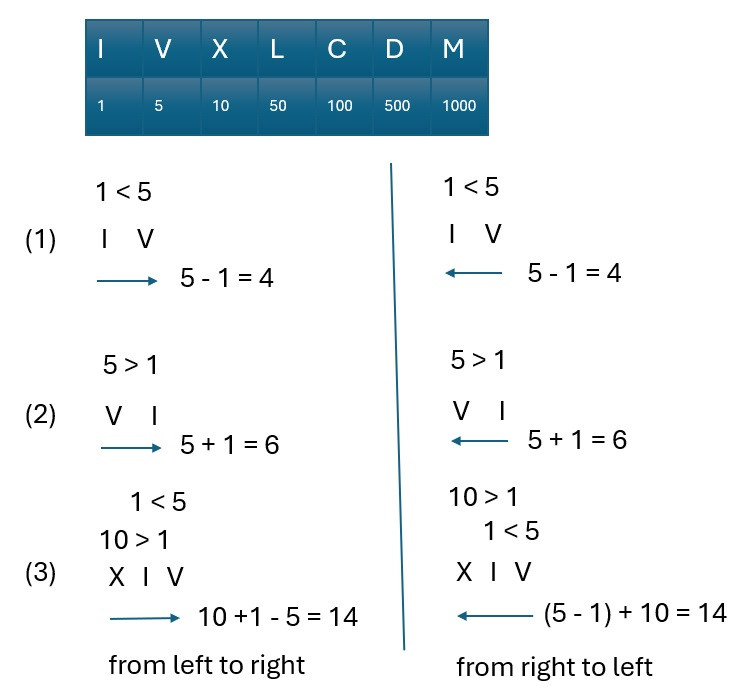

讓我們根據上面的討論，分別實現從左往右計算和從右往左計算羅馬數字的代碼。
從左往右:

var romanToInt = function(s) {
    const romanToIntMap = {
        'I': 1,
        'V': 5,
        'X': 10,
        'L': 50,
        'C': 100,
        'D': 500,
        'M': 1000
    };

    let result = 0;

    for (let i = 0; i < s.length; i++) {
        const currentValue = romanToIntMap[s[i]];
        const nextValue = romanToIntMap[s[i + 1]];

        if (nextValue > currentValue) {
            result -= currentValue;
        } else {
            result += currentValue;
        }
    }

    return result;
};

從右往左:

var romanToInt = function(s) {
    const romanToIntMap = {
        'I': 1,
        'V': 5,
        'X': 10,
        'L': 50,
        'C': 100,
        'D': 500,
        'M': 1000
    };

    let result = 0;
    let prevValue = 0;

    for (let i = s.length - 1; i >= 0; i--) {
        const currentValue = romanToIntMap[s[i]];
        if (currentValue < prevValue) {
            result -= currentValue;
        } else {
            result += currentValue;
        }
        prevValue = currentValue;
    }

    return result;
};

時間複雜度：O(n)，其中 n 是羅馬數字字符串的長度。我們需要遍歷字符串中的每一個字符。
空間複雜度：O(1)，只使用了常數級別的額外空間來存儲結果和映射表。

總結：
無論是從左和右或是從右往左，這兩個方法在時間和空間複雜度上幾乎沒有區別，都是 O(n) 的時間複雜度和 O(1) 的空間複雜度。然而，這兩者在程式執行邏輯上略有不同，從左往右方法是從頭到尾遍歷並檢查下一個字符的值，從右往左方法是從字串的末尾開始遍歷。在某些情況下，從右往左方法可能略微更有效率，因為它避免了在每次迴圈中檢查下一個字符的值。
對於這道題，我們可以將其歸類為「for 迴圈」。雖然這是一道基礎的練習題，但希望讀者能夠確實掌握這兩種 for 迴圈的遍歷方式。這將為後續的 LeetCode 學習打下堅實的基礎，讓我們能夠在更加複雜的問題中應用這些基本技巧繼續前進學習。